1tique occurrentibus in H& I.Secetur tangens in A,ita ut ſit
HAad AI,ut eſt rectan
 52[Figure 52]
52[Figure 52]
gulum ſub media proportio
nali inter CG& GP& me
dia proportionali inter BH&
HD,ad rectangulum ſub me
dia proportionali inter DG&
GB& media proportionali in
ter PI& IC; & erit Apunc
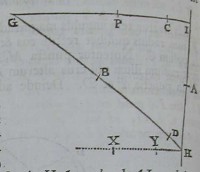
tum contactus. Nam ſi rectæ
PIparallela HXTrajecto
riam ſecet in punctis quibuſ
vis X& Y:erit (ex Conicis)
punctum Aita locandum, ut fuerit HA quad.ad AI quad.in ra
tione compoſita ex ratione rectanguli XHYad rectangulum BHD
ſeu rectanguli CGPad rectangulum DGB& ex ratione rectan
guli BHDad rectangulum PIC.Invento autem contactus
puncto A,deſcribetur Trajectoria ut in caſu primo. q.E.F.
Capi autem poteſt punctum Avel inter puncta H& I,vel extra;
& perinde Trajectoria dupliciter deſcribi.
HAad AI,ut eſt rectan
 52[Figure 52]
52[Figure 52]gulum ſub media proportio
nali inter CG& GP& me
dia proportionali inter BH&
HD,ad rectangulum ſub me
dia proportionali inter DG&
GB& media proportionali in
ter PI& IC; & erit Apunc
tum contactus. Nam ſi rectæ
PIparallela HXTrajecto
riam ſecet in punctis quibuſ
vis X& Y:erit (ex Conicis)
punctum Aita locandum, ut fuerit HA quad.ad AI quad.in ra
tione compoſita ex ratione rectanguli XHYad rectangulum BHD
ſeu rectanguli CGPad rectangulum DGB& ex ratione rectan
guli BHDad rectangulum PIC.Invento autem contactus
puncto A,deſcribetur Trajectoria ut in caſu primo. q.E.F.
Capi autem poteſt punctum Avel inter puncta H& I,vel extra;
& perinde Trajectoria dupliciter deſcribi.
DE MOTU
CORPORUM
CORPORUM
PROPOSITIO XXIV. PROBLEMA XVI.
Trajectoriam deſcribere quæ tranſibit per data tria puncta & rectas
duas poſitione datas continget.
duas poſitione datas continget.
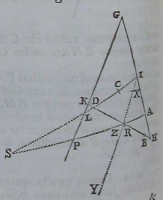
Dentur tangentes HI, KL&
 53[Figure 53]
53[Figure 53]
puncta B, C, D.Per punctorum
duo quævis B, Dage rectam in
finitam BDtangentibus occur
rentem in punctis H, K.Deinde
etiam per alia duo quævis C, D
age infinitam CDtangentibus oc
currentem in punctis I, L.Actas
ita ſeca in R& S,ut ſit HRad
KRut eſt media proportionalis
inter BH& HDad mediam
proportionalem inter BK& KD;
& ISad LSut eſt media pro
portionalis inter CI& IDad me
diam proportionalem inter CL
 53[Figure 53]
53[Figure 53]puncta B, C, D.Per punctorum
duo quævis B, Dage rectam in
finitam BDtangentibus occur
rentem in punctis H, K.Deinde
etiam per alia duo quævis C, D
age infinitam CDtangentibus oc
currentem in punctis I, L.Actas
ita ſeca in R& S,ut ſit HRad
KRut eſt media proportionalis
inter BH& HDad mediam
proportionalem inter BK& KD;
& ISad LSut eſt media pro
portionalis inter CI& IDad me
diam proportionalem inter CL
